基于MATLAB的复杂系统仿真研究与应用(matlab程序)
基于MATLAB的复杂系统仿真研究与应用(matlab程序)(课题申报表,任务书,开题报告,中期检查表,外文翻译,论文20000字,程序,答辩PPT)
摘 要
随着社会和经济的发展，系统科学工作者面临的研究对象也越来越复杂，迫切需要进行复杂系统的仿真与研究。
复杂系统具备高阶次、多回路、非线性、多时标、层次性、开放性、不确定性、病态结构, 以及涌现等特点。本文列举了四个典型的复杂系统：混沌系统，分数阶系统，时滞系统和不确定系统，并着重于应用MATLAB对其进行系统仿真，其中列举了采用Runge—Kutta法在MATLAB里调用ode45公式进行Rossler混沌系统的编程，用SIMULINK进行Lorenz混沌系统的编程，用dde23方式进行时滞系统微分方程的编程，用S函数与SIMULINK相结合进行不确定系统的仿真等。本文也简单的介绍了混沌系统，分数阶系统，时滞系统和不确定系统的特点，以及它们在各领域中的应用。
关键词：混沌系统；分数阶系统；不确定系统；时滞系统；MATLAB
Abstract
With the social and economic development,the objects which scientific system workers faced are becoming more and more complex,the need for simulation and study of complex systems is urgent. [资料来源：http://Doc163.com]
The characteristics of complex system are higher order,multi-loop,nonlinear,long-labeled,hierarchy,openness,uncertainty,ill-structured,and the emergence and so on.This paper lists several typical complex system,such as chaotic systems,fractional systems,delay systems and uncertain systems,and applied MATLAB to carry out the system simulation.Which lists Rossler chaotic system programming mode with ode45 by the method of Runge—Kutta,Lorenz chaotic systems withSIMULINK,differential equations of delay system with edd23,uncertain systems simiulation with s-function and SIMULINK and so on. This paper also simply introduces the chaos system, the fractional order system, the time-delay system,the uncertain system and their characteristics and application in various fields.
Key words: chaotic systems; fractional systems; delay systems; uncertain systems ; MATLAB
本文重点列举了四种复杂系统：混沌系统，分数阶系统，时滞系统，不确定系统。分别介绍了它们的出现背景，独有特点，以及发展情况。本文侧重于对于这四个系统的MATLAB仿真，运用建立m文件以及S函数与SIMULINK相结合的方法。 [资料来源：http://www.doc163.com]
全文的主要工作如下：
（1）简单的介绍了课题的研究意义，复杂系统的基本概念、特点以及MATLAB的基本组成。
（2）根据复杂系统的特点，首先举出了混沌系统，混沌系统的一大特点就是对初值的极度敏感，非线性是产生混沌的必要条件。在MATLAB中应用Runge—Kutta法对混沌系统进行相图绘制。
（3）其次列举了分数阶系统，分数阶系统是建立在分数阶微积分以及分数阶微分方程理论上的模型系统。简单介绍了Gamma函数、Beta函数和Mittag-Leffler函数。在MATLAB对去进行仿真时，我们用的是传递函数表达的，利用建立新的主函数，来进行函数的调用。
（4）提出了时滞系统，时滞微分方程的一般形式是泛函微分方程，它是无限维的。我们用MATLAB中的dde23公式来进行带有时滞的微分方程的的仿真。
（5）根据复杂系统的不确定性，我们这里提出了不确定系统。介绍了研究不确定系统的随机控制、自适应、鲁棒控制、变结构控制、模糊控制、神经网络控制，以及这六种策略的优缺点。应用S函数与SIMULINK相结合的方法进行的不确定系统的仿真。
[资料来源：www.doc163.com]
目 录
第1 章 概述 1
1.1 课题研究的基本意义 1
1.2 本文主要研究内容 1
1.3 系统的基本概念 1
1.4 复杂系统的概念及特点 2
1.5 复杂系统理论的介绍 3
1.6 仿真技术的意义 4
1.7 仿真的算法 5
1.8 仿真技术的发展情况 6
1.9 MATLAB相关介绍 7
第2章 混沌系统 8
2.1 混沌系统的背景介绍 8
2.2 混沌系统的特点 8
2.3 混沌系统的同步问题 9
2.4 混沌系统的应用及发展 10
2.5 混沌系统的相图绘制 11
2.6 本章小结 15
第3章 分数阶系统 16
3.1 分数阶系统的基本介绍 16
3.2 分数阶系统的基本函数 16
3.3分数阶系统的描述形式 18
3.4分数阶系统的应用及发展 20
3.5 分数阶系统的仿真 21
3.6 本章小结 23
第4 章 时滞系统 24
4.1 时滞系统的概述 24
4.2 时滞系统的特点 27
4.3 时滞系统的应用 29
4.4 时滞系统的仿真 29
4.5 本章小结 30
第5章 不确定系统 31
5.1 不确定系统的介绍 31
5.2 不确定系统的特点及研究方法 32
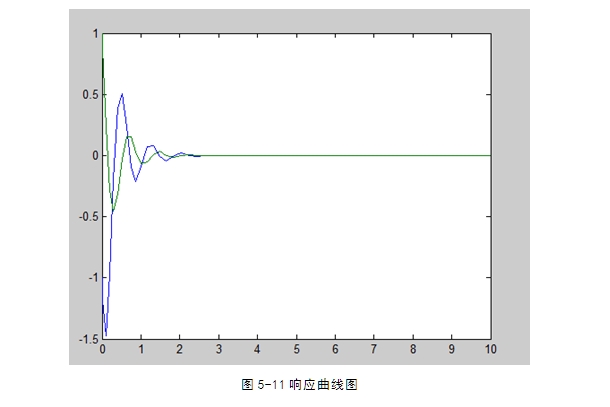
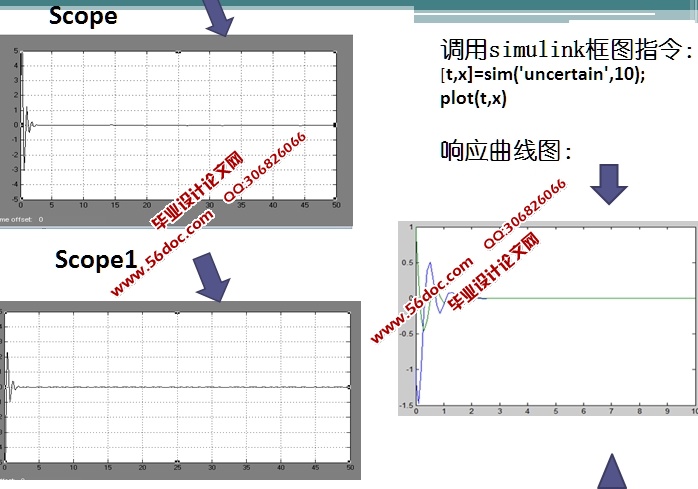
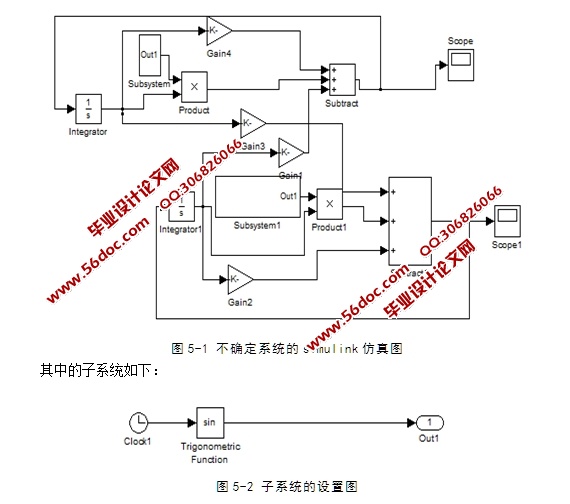
5.3不确定系统的仿真实例 33
5.4 本章小结 38
结论 39
参考文献 40
致 谢 42