传染病微分方程模型的研究
传染病微分方程模型的研究(8200字)
摘 要：本文以微分方程为工具，对现有基本的传染病模型进行了研究。利用微分方程的稳定性理论对各系统无病平衡点和地方平衡点的存在性及稳定性进行了定性的讨论，利用matlab软件做出了各系统的S-I相轨线图。以SARS为例，分析了传染病模型对疾病的控制、预防所起的指导性作用。以北京市的SARS传播数据为依据，从经典的SI传染病模型入手，预测了疾病的高峰期，首例病人发病日期；利用matlab 软件，分析了控制前的SIR模型，以此预测了政府不加控制的最高发病人数；通过机理分析，控制后的模型充分考虑了SARS传染病的多个因素，建立了5类人的疫情传播的模型，并有效合理地拟合了变量参数，假设了控制参数，得到了预测曲线。
关键词：传染病模型;微分方程;曲线拟合
Differential Equation Model of Infectious Diseases
Abstract: In this paper, utilizing differential equation, the basal epidemic models were studied. Using stability theory in differential equation the existence and the stability of the equilibrium are discussed. Using software of Matlab the phase orbit of every system is devised. Taking SARS as an example, we can see epidemic model can play a leading effect on preventing diseases and controlling diseases. According to the spread data of SARS in Beijing, utilizing classical epidemic model, the morbid fastigium and the date of first patient are doped out. SIR epidemic model is meet for the initial epidemic period, and the maximum amount of patients without control is forecasted with Matlab. Through thinking about main factors to the influence, the dubious category and the taking pathogen category are imported, so the model of five categories is founded. In the model variate parameters are simulated reasonably and control parameters are hypothesized．And the forecasting curves which are fit for the situation are also made.
Keywords: epidemic model; differential equation; cure fitting
本文的主要工作
首先，本文以微分方程为工具，从最基本的传染病模型出发，分析流动人口及预防接种对传染病传播的影响，假设迁入率为常数 ，迁出率为常数 ，比例接种率为 ，建立SIR传染病模型，然后讨论几个参数对疾病传播的影响，利用微分方程的稳定性理论对各系统无病平衡点和地方病平衡点的存在性及稳定性进行定性的讨论。利用Matlab软件作出各系统的 ，相图，根据图像可以直观的看出各参数对得病人数的影响。其次，以SARS为例，以北京市的SARS传播数据为依据，以传统的微分方程理论为基础，从经典的SI传染病模型入手，预测疾病的高峰期，首例病人发病日期。利用Matlab软件，分析控制前的SIR模型，以此预测政府不加控制的最高发病人数；通过机理分析，控制后的模型充分考虑对SARS流行有较大影响的多个因素，引入疑似病例及非控带菌者，建立5类人的描述疫情传播的模型，并且较合理地拟合变量参数，假设控制参数，得到各类人的预测曲线。这些结论对于传染病的预防以及控制可以起到一定的借鉴作用。
[资料来源：http://Doc163.com]
目 录
摘要……………………………………………………………………………………1
关键词…………………………………………………………………………………1
1前言…………………………………………………………………………………2 [资料来源：Doc163.com]
1.1数学模型的慨念…………………………………………………………………2
1.2传染病模型的研究意义…………………………………………………………3
1.3本文的主要工作…………………………………………………………………4
2 几种基本的传染病模型……………………………………………………………4
2.1 SI模型：不考虑病人治愈的传染病模型………………………………………4
[来源：http://Doc163.com]
2.1.1模型的建立及求解……………………………………………………………4
2.1.2 模型检验………………………………………………………………………6
2.2 SIS模型：病人可以治愈但无免疫力的传染病模型…………………………6
2.3 SIR模型：病人可以治愈且有免疫力的传染病模型…………………………8
2.3.1模型建立及求解………………………………………………………………8
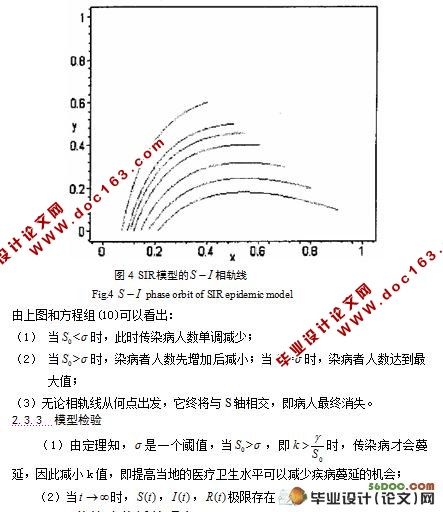
2.3.2 的相轨线图………………………………………………………………9
[资料来源：www.doc163.com]
2.3.3模型检验………………………………………………………………………10
3 SARS传染病传播的研究…………………………………………………………10
3.1用SI模型求解……………………………………………………………………11
3.1.1 拟合累计确诊病例……………………………………………………………11
3.1.2 推测发病高峰期………………………………………………………………12 [资料来源：https://www.doc163.com]
3.1.3 推测首例发病日期……………………………………………………………12
3.2控制前的SARS传染病模型……………………………………………………12
3.2.1理论上染病者的最大数量……………………………………………………13
3.2.2控制 的值……………………………………………………………………13
3.3控制后的SARS传染病模型……………………………………………………14
3.3.1模型假设………………………………………………………………………14
3.3.2符号说明及定义………………………………………………………………14
3.3.3 模型建立………………………………………………………………………14
3.3.4 参数的确定……………………………………………………………………15
3.3.5模型的求解……………………………………………………………………18 [资料来源：Doc163.com]
4 总结…………………………………………………………………………………21
4.l本文的主要结论…………………………………………………………………21
4.2进一步研究方向…………………………………………………………………21
参考文献………………………………………………………………………………21
致谢……………………………………………………………………………………23 [来源：http://www.doc163.com]